0. Spanning Tree
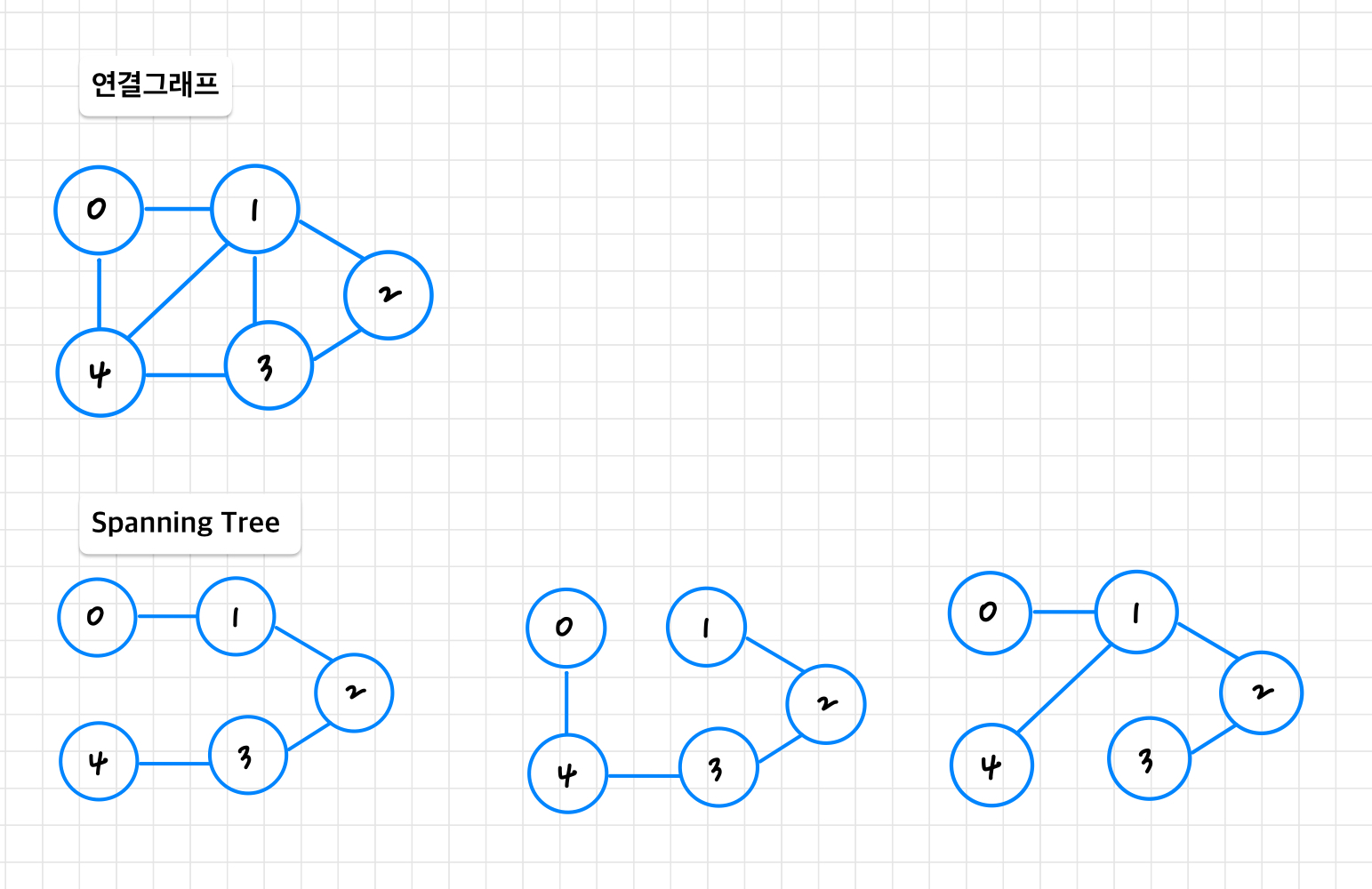
Spanning Tree란 그래프 내의 모든 정점을 포함하는 트리입니다. 즉, 그래프에서 일부 간선을 선택해서 만든 트리입니다. 이때 그래프에 사이클이 형성이 되면 안됩니다. 연결 그래프에 대한 spanning tree는 여러개 일 수 있습니다.
n개의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개이고, (n-1)개로 연결되어 있으면 필연적으로 트리 형태가 되고 이것이 spanning tree가 됩니다. 따라서 spanning tree는 그래프에 있는 n개의 정점을 (n-1)개의 간선으로 연결합니다.
1. Minimum Spanning Tree (MST)
MST는 트리를 구성하는 간선들의 가중치를 합한 것이 최소가 되는 신장 트리이며 다음의 조건을 충족해야합니다.
- 최소 비용의 간선으로 구성
- 사이클을 포함하지 않음
MST를 구하는 방법들은 greedy algorithm으로 구현이 되어 있습니다. 대표적인 것에는 Kruskal Algorithm과 Prim Algorithm이 있습니다.
2-1. Kruskal MST Algorithm
0) 정의
Kruskal은 간선 선택을 기반으로 하는 알고리즘입니다. 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법입니다.
1) 과정
[1] 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
[2] 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.
[3] 해당 간선을 현재의 MST의 집합에 추가한다.
- 그림 설명

2) code
#kruskal algorithm
parent = dict() # 각 정점의 root node(부모)를 표현한 배열
rank = dict()
#node 초기화
def make_set(node):
parent[node] = node
rank[node] = 0
#해당 node의 최상위 정점을 찾는다 (가장 낮은 가중치 선택)
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
#두 정점을 연결한다
def union(node1, node2):
root1 = find(node1)
root2 = find(node2)
if root1 != root2:
if rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2] += 1
def kruskal(graph):
minimum_spanning_tree = []
#초기화
for node in graph['nodes']:
make_set(node)
#1) 간선 weight 기반 sorting
edges = graph['edges']
edges.sort() #오름차순 정렬
#2) 간선 연결 (사이클 없게)
for edge in edges:
weight, node1, node2 = edge
#만약 사이클이 발생하지 않는다면 (node1과 node2의 최상위 정점이 같지 않다면)
if find(node1) != find(node2):
#루트노드가 다르므로 union
union(node1, node2)
#3) 간선 추가
minimum_spanning_tree.append(edge)
return minimum_spanning_tree
def solution():
graph = {'nodes': [1, 2, 3, 4],
'edges': [(1,1,2),(1,1,3),(1,2,3),(1,3,4),(3,2,4)]} #(weight,node1,node2)
return kruskal(graph)
solution()
# 결과 : [(1, 1, 2), (1, 1, 3), (1, 3, 4)]
# 가중치의 합 : 3
2-2. Prim MST Algorithm
0) 정의
Prim은 정점 선택을 기반으로 하는 알고리즘입니다. 이전 단계에서 만들어진 신장 트리를 확장하는 방법입니다.
1) 과정
[1] 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
[2] 앞 단계에서 만들어진 MST집합에 인접한 정점들 중에서 최소 간선으로(가장 낮은 가중치로) 연결된 정점을 선택하여 트리를 확장한다.
[3] (n-1)개의 간선을 가질 때까지 반복한다.
2) code
- edge 탐색을 위해 min heap 을 이용한 priority queue를 사용합니다. priority queue는 우선 순위가 가장 높은 자료를 가장 먼저 꺼낼 수 있는 자료 구조입니다. python에서는 이를 구현한 heapq 라이브러리가 있습니다.
#prim algorithm
from collections import defaultdict
from heapq import *
def prim(first_node, graph):
minimum_spanning_tree = []
adjacent_edges = defaultdict(list)
for weight, node1, node2 in graph:
adjacent_edges[node1].append((weight, node1, node2))
adjacent_edges[node2].append((weight, node2, node1))
connected = set(first_node)
candidated_edge = adjacent_edges[first_node]
heapify(candidated_edge)
while candidated_edge:
weight, node1, node2 = heappop(candidated_edge)
if node2 not in connected:
connected.add(node2)
minimum_spanning_tree.append((weight, node1, node2))
for edge in adjacent_edges[node2]:
if edge[2] not in connected:
heappush(candidated_edge, edge)
return minimum_spanning_tree
def solution():
graph = [(1,'1','2'),(1,'1','3'),(1,'2','3'),(1,'3','4'),(3,'2','4')]
return prim('1',graph)
solution()
#결과 : [(1, '1', '2'), (1, '1', '3'), (1, '3', '4')]